Unity DOTS学习笔记(二)SoftBody2D软体物理
写物理的过程就是心态跟着几何体的不停崩裂而崩裂。
上个月心血来潮想做个2d软体物理的PinBall Game。于是上网找了一些软体物理教程就开始动手搞了。但整个过程就是实现效果一两天,后期踩坑一个月,心态崩的怀疑人生。
弹簧质点是当前主流的物理实现方式之一。我看到youtube有完整公式介绍,就开始直接按这套函数在dots里实现。
参考:
https://lisyarus.github.io/blog/physics/2023/05/10/soft-body-physics.html
首先,软体的数据格式可以是这样:
- 一个软体的容器:SoftBody
- 其下有若干的质点:Point
- 其下又有若干弹簧:Spring,记录了连接的2个Point的id
然后,简单来说整个软体解算过程就是:

- 定义一个力F
- 每帧给F加上重力,弹簧力,碰撞挤压力,等其他一些力
- 将F叠加到质点已有的Velocity上
- 将最终的Velocity应用到质点坐标上
其中Spring弹力的计算需要考虑到弹簧的刚性和衰减,公式如下:
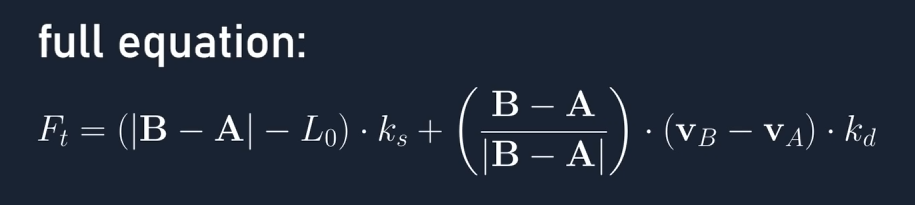
而碰撞检测的方式是:
- 在前一帧的结尾计算每个碰撞体的AABB:遍历一个SoftBody下的所有Point的坐标,找出最大最小值。
- 在当前帧,先检测软体的AABB是否相交,相交则继续做碰撞检测
- 由当前质点发射任意方向一条射线,与目标软体的每个边检测是否相交,算出总的交点数量。总数是奇数则质点在目标软体内部,总数是偶数则质点在目标软体外。
- 如果质点在目标软体内,则计算质点与每条边的最短距离和交点,最后得出的必然是某条边的垂线的交点。然后计算出挤出力Velocity。
“射线相交检测“和”点与线段最短距离“的代码参考:
bool RayToLineSegment(float2 rayStart, float2 rayDir, float2 lineA, float2 lineB)
{
float2 lineA2B = lineB - lineA;
float2 ray2A = rayStart - lineA;
float r, s, d;
//Make sure the lines aren't parallel, can use an epsilon here instead
// Division by zero in C# at run-time is infinity. In JS it's NaN
if (rayDir.y / rayDir.x != lineA2B.y / lineA2B.x)
{
d = rayDir.x * lineA2B.y - rayDir.y * lineA2B.x;
if (d != 0)
{
r = (ray2A.y * lineA2B.x - ray2A.x * lineA2B.y) / d;
s = (ray2A.y * rayDir.x - ray2A.x * rayDir.y) / d;
if (r >= 0 && s >= 0 && s <= 1)
{
return true;
}
}
}
return false;
}
float2 PointToSegmentClosestPosition(float2 point, float2 lineA, float2 lineB)
{
float2 v = lineB - lineA;
float2 w = point - lineA;
float c1 = math.dot(w, v);
if (c1 <= 0) // before lineA
return lineA;
float c2 = math.dot(v, v);
if (c2 <= c1) // after lineB
return lineB;
float b = c1 / c2;
return lineA + b * v;
}以上是主动式计算过程,按这个方式写下去,很快就能实现效果,但软体数量多了以后,经常会在计算复杂弹性的时候奔溃。心态要炸呀。

后来老老实实搜了几篇软体相关论文,发现其实已经有人总结了这个问题。主动式的计算方式必然会在极端情况下崩掉,有数学论文论证过。(反正我也不懂)
然后就有了被动式的计算方式:Position-Based Dynamic。简称(PBD)这个作者搞了不少好东西。参考:https://matthias-research.github.io/pages/tenMinutePhysics/

其连接里有demo演示和完整代码。据说PBD也被用在不少主流引擎物理系统里。
大致解算过程如下:

- 因为奔溃的罪魁祸首就是弹性,所以先忽略弹性计算。每帧一开始根据质点重力,velocity和碰撞计算出质点最终的坐标。
- 然后再计算弹性影响,去修正质点的坐标。弹性的计算也进行了简化。并且要分多次迭代去修正,因为单次计算的话,每个弹簧的力都比较大,叠加到一起容易出现大误差造成崩溃。而迭代多次,每次算出一个小小的力来修正质点,就可以尽量避免崩溃了。
- 最后经过修正的质点坐标减去上一帧的坐标,就直接当作了质点的velocity。
以上过程据说是有复杂数学公式证明的,是一个快速收敛的公式,不会导致崩溃。(反正我也不懂)
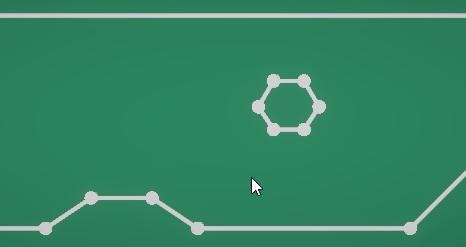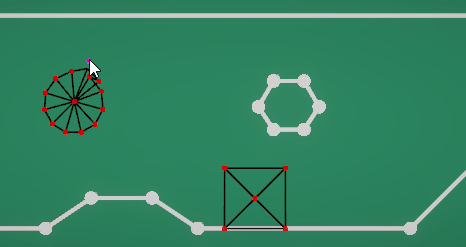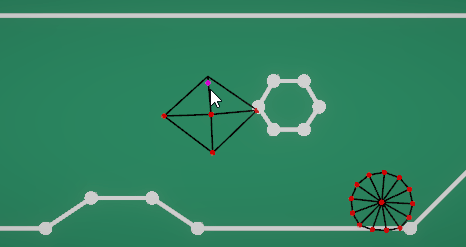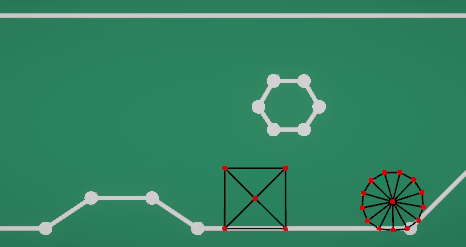
而PBD的计算过程再dots里实现起来还是一样轻松。其结果也是对得起我踩了一个月的坑好吧。
最后再聊聊Shape Matching和Pressure
Shape Matching-形状匹配
用一个模型框架来约束软体外形。软体边缘的每个质点都用长度为0的spring连接到框架上。
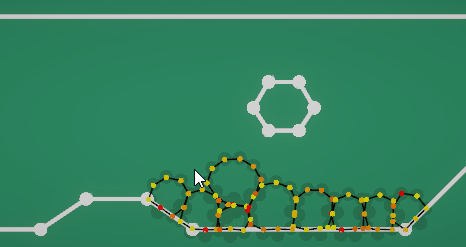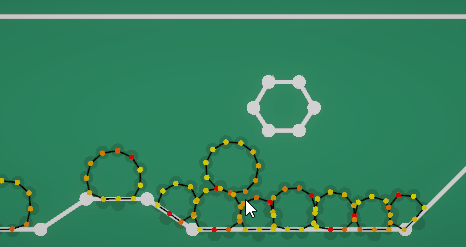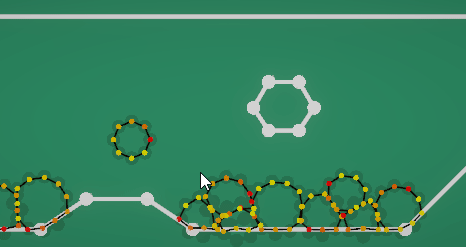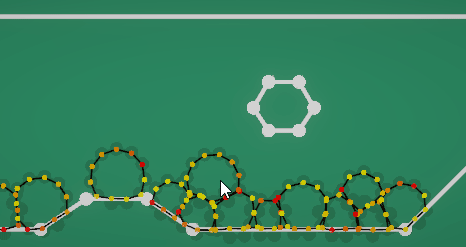
由于这个力会影响碰撞挤压,所以这个弹簧约束的计算可以放在碰撞检测之前的预计算里,不用参与到后续的弹性约束。因为每个质点只有一根弹簧连到框架上,所以这份弹力也不会应为复杂的弹簧计算而崩溃。(如上图中每个圆形软体背后有个浅色的框架)
在每一帧的结尾,用当前的质点坐标计算出框架的坐标和旋转。方式如下:
- 框架中点的坐标 = 所有质点坐标之和 / 质点数量;
- 框架的旋转角度 = 所有质点相对于初始重心点的角度偏移的平均值
Shape外框跟随软体变换坐标和旋转的参考代码:
// 计算软体重心
float2 centerPos = float2.zero;
foreach (var point in shapePoints)
{
centerPos += point.position;
}
centerPos /= shapePointCount;
// 计算软体的旋转
float A = 0.0f, B = 0.0f;
foreach (var point in shapePoints)
{
float2 dir = point.position - centerPos ;
A += math.dot(dir , point.originPosition); // originPosition是软体初始化时相对于重心的初始坐标
B += dir.x * point.originPosition.y - dir.y * point.originPosition.x;
}
float angle = -math.atan2(B, A); // 这里算出的是整个软体的旋转角度
// update new shape position
foreach (var point in shapePoints)
{
point.position = centerPos + rotate(point.originPosition, angle); // 设置shape每个质点的新坐标
}Perssure-外形挤压
先计算每条边的法线方向,然后每帧传递给关联的两个质点,让软体像气球一样膨胀。这种方式比较适合圆形球体。
这个Perssure Force的计算也是放在预计算碰撞之前。
弹性线条
由于上述物理碰撞的计算只试用于闭合形状,对于单个线条是无法知道点是否在形状内部的。把物理碰撞检测改成点对于线段的物理碰撞我也尝试过,一旦遇到多根线条交叉在一起的情况,碰撞就很不准确,我也没有找到很好的解决方案。所以我目前的做法是:
- 软体绳索(Rope):只处理线条的点对于所有软体/刚体的碰撞,且每个点的半径足够大,能包裹住线条,避免碰撞时穿帮。
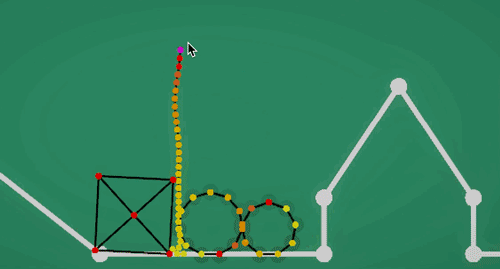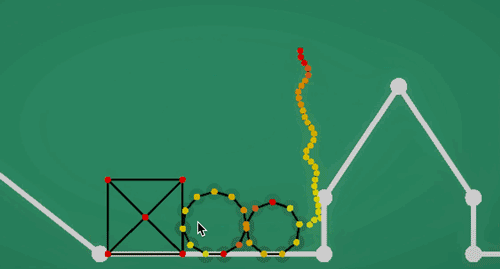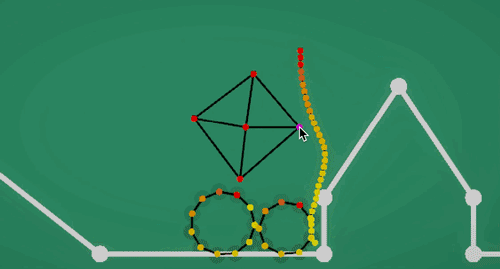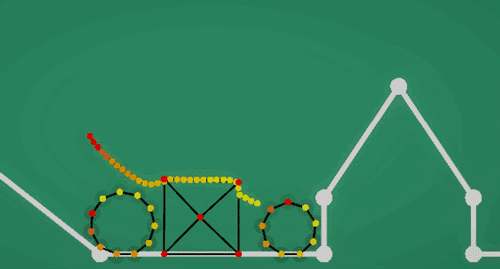
- 绷紧的弦(String):用封闭软体,利用交叉弹簧特性保持形状稳定,两头固定住不动,可以做为弹簧跳板之类的玩法。
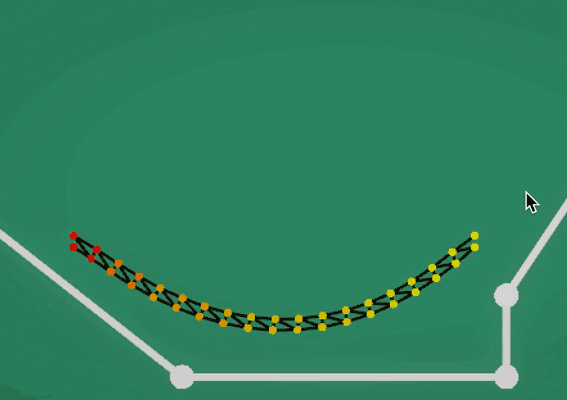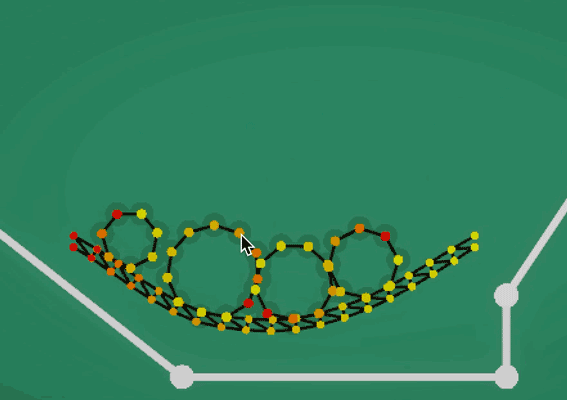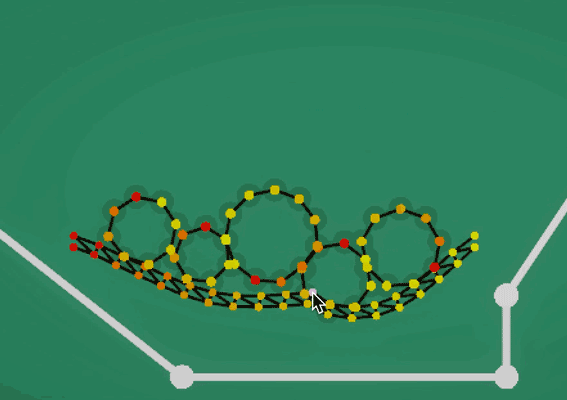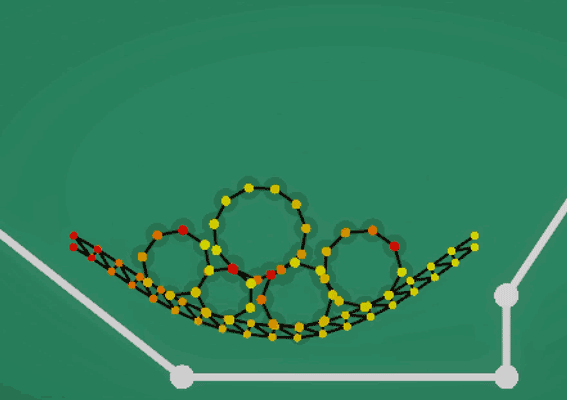
总结
以上就是我目前在网上找到的几种软体物理的做法。利用DOTS的多线程解算可以同屏跑几十个软体不成问题。可以做一些RocoLoco类型的小游戏了。